Cet article est disponible sous forme d’iBook sur l’iBookStore (iOS & OSX) https://itunes.apple.com/fr/book/le...
1. Introduction
L’émergence des ordinateurs, accélérée par la seconde Guerre mondiale, a donné une nouvelle dimension aux « mathématiques expérimentales » c-à-d l’exploration des propriétés d’objets mathématiques par des calculs.
Cette approche qui a toujours existé, avait vu son importance diminuer progressivement à partir du XVIIe siècle en raison de la place grandissante de l’abstraction.
Au-delà de l’extension stupéfiante du domaine des calculs possibles, de leur vitesse et de leur précision, les ordinateurs ont fourni un outil puissant : la visualisation, qui permet une exploration et la découverte de phénomènes qui passeraient inaperçus autrement.
Les sciences physiques ont tiré un bénéfice des ordinateurs encore plus grand et plus profond que les mathématiques : les ordinateurs permettent de faire des expériences numériques à partir des équations gouvernant les phénomènes que l’on désire étudier, alors que les expériences classiques peuvent être trop compliquées, trop coûteuses, voire impossibles à réaliser (comme en astrophysique). Des expériences -dans le monde « réel »- ont même été suscitées par des expériences numériques (nous en verrons des exemples).
Le terme anglo-saxon pour qualifier cette approche est « simulation », qui est également utilisé par les francophones. Mais le mot « expérimentation » correspond beaucoup mieux à ce qu’est effectivement l’utilisation du numérique dans ces sciences.
L’objet de ce livret est de montrer comment l’expérimentation numérique -devenue interactive au fil du temps- a permis des découvertes impossibles sans elle, ainsi que le renouvellement, voire la renaissance, de certains domaines des mathématiques et de la physique. Au-delà du monde de la recherche scientifique, les ordinateurs ont évidemment influencé la didactique des mathématiques et de la physique (par exemple la théorie qualitative des équations différentielles).
Les grands inspirateurs de l’utilisation de l’expérimentation numérique sont Stanislas Ulam, John von Neumann et Alan Turing. Partant de ces figures incontournables, nous évoquerons plusieurs exemples, plus ou moins célèbres, qui illustrent cette démarche.
Sommaire
![]() 1. Introduction
1. Introduction
![]() 2. John von Neumann & Stanislas Ulam
2. John von Neumann & Stanislas Ulam
![]() 3. Enrico Fermi, John Pasta, Stanislas Ulam & Mary Tsingou
3. Enrico Fermi, John Pasta, Stanislas Ulam & Mary Tsingou
![]() 4. La morphogenèse selon Alan Turing
4. La morphogenèse selon Alan Turing
![]() 5. Bryan Birch & Peter Swinnerton-Dyer & les points rationnels des courbes elliptiques
5. Bryan Birch & Peter Swinnerton-Dyer & les points rationnels des courbes elliptiques
![]() 6. Edward Lorenz : de la météo aux attracteurs étranges
6. Edward Lorenz : de la météo aux attracteurs étranges
![]() 7. Martin Kruskal & Norman Zabusky découvrent numériquement les solitons
7. Martin Kruskal & Norman Zabusky découvrent numériquement les solitons
![]() 8. Michel Hénon : de l’astrophysique aux attracteurs étranges
8. Michel Hénon : de l’astrophysique aux attracteurs étranges
![]() 9. La cascade de doublements de période : Mitchell Feigenbaum, Pierre Coullet & Charles Tresser
9. La cascade de doublements de période : Mitchell Feigenbaum, Pierre Coullet & Charles Tresser
![]() 10. Itérations de polynômes complexes : Benoît Mandelbrot, John Hubbard & Adrien Douady
10. Itérations de polynômes complexes : Benoît Mandelbrot, John Hubbard & Adrien Douady
![]() Quelques références bibliographiques
Quelques références bibliographiques
![]() Références « historiques »
Références « historiques »
![]() Carte du monde des expériences numériques citées
Carte du monde des expériences numériques citées
++++
2. John von Neumann & Stanislas Ulam
John von Neumann et Stanislas Ulam sont les premiers à avoir compris le potentiel des ordinateurs en mathématique et en physique :
- Stanislas Ulam
« Presque immédiatement après la guerre, John von Neumann et moi-même avons commencé à discuter la possibilité d’utiliser les ordinateurs de façon heuristique, pour essayer d’obtenir quelques lumières sur des questions de mathématiques pures. En produisant des exemples et en observant les propriétés de certains objets mathématiques, on peut espérer obtenir des éléments de réponse quant au comportement des lois générales. Lors des années qui ont suivi j’ai suggéré, et dans certains cas résolu, une variété de problèmes de mathématiques pures en expérimentant ou même tout simplement en observant » (sous entendu “au moyen de l’ordinateur”)
(Extrait de son autobiographie : Adventures of a Mathematician, 2d ed., Berkeley, 1991)
Il propose donc d’utiliser les ordinateurs non pas comme un simple « moulin » à calculs mais comme un outil d’expérimentation permettant de « voir » les solutions des équations que l’on étudie. La vision d’Ulam a été motivée par la physique, plus précisément l’étude numérique de modèles simplifiés de diffusion des neutrons (liés à la bombe atomique). Notons que les premiers calculs pour une réaction en chaîne sont réalisés par Nicholas Metropolis en 1947, sur l’ENIAC et qu’il s’agit des prémisses de la méthode de Monte-Carlo. (La méthode de Monte-Carlo naît officiellement dans un article de Metropolis et Ulam en 1949.) Nous verrons un autre exemple issu de la physique plus bas (mécanique statistique).

- John von Neumann (1952)
Dans un texte écrit en 1947 et intitulé « The Mathematician », von Neumann se demande si les mathématiques sont une science empirique. Il tente de répondre à cette question par une confrontation avec les démarches de la physique théorique. Pour lui, il y a une base empirique aux mathématiques, occultée par les développements ultérieurs, mais « quand des tendances à devenir baroque se font jour, le signal de danger doit être émis » et le seule remède semble être, selon lui, la ré-injection d’idées plus ou moins directement empiriques. Cette réflexion, qui fait le bilan de ses travaux depuis 1922, explique en partie le développement du calcul numérique et des mathématiques expérimentales. Dans cet esprit, Ulam cherche à développer une pratique des expériences numériques, d’abord dans le domaine de la combinatoire et de la théorie des nombres, puis dans domaine du « non linéaire » où il explore avec ses collaborateurs les comportements de diverses transformations non linéaires. Un des modèles est celui de l’évolution d’une grande population dans laquelle se produisent des accouplements aléatoires et des mutations. Il ne s’agit pas d’équations différentielles mais d’itérations d’une transformation non linéaire. Ces analyses sont destinées à ouvrir des perspectives, à poser des problèmes plutôt qu’à en résoudre. Notons que l’ordinateur est branché à un système permettant la visualisation des itérations. Il s’agit ni plus ni moins d’une nouvelle façon d’étudier les itérations non linéaires qui nous paraît aujourd’hui évidente…
++++
3. Enrico Fermi, John Pasta, Stanislas Ulam & Mary Tsingou
A Los Alamos, au début des années 1950, Enrico Fermi, John Pasta et Stanislas Ulam proposent un modèle pour comprendre l’évolution vers l’équilibre thermique dans un cristal. Leur modèle est suffisamment simple pour être étudier avec un ordinateur de l’époque.
|
|
|
Il s’agit d’une chaîne unidimensionnelle de masses identiques reliées entre elles par des ressorts. Quand on écarte une masse de sa position d’équilibre, elle subit une force de rappel qui n’est pas proportionnelle à la distance au point d’équilibre. Ce modèle est différent de celui étudié dans les cours de physique où il y a proportionnalité (on parle de chaîne « harmonique » d’oscillateurs, ce qui rend le modèle « linéaire » et donc résoluble). Même la faible « anharmonicité » introduite par Fermi, Pasta et Ulam rend le modèle très compliqué et nécessite son exploration par une expérience numérique, sans doute la première du genre. Ils considèrent 16, 32 puis 64 masses.

- Ordinateur Maniac I
À leur grande surprise, ils découvrent que le système, au lieu de tendre vers l’équipartition de l’énergie (synonyme de thermalisation), présente au contraire des solutions quasi-périodiques, en contradiction avec l’hypothèse ergodique qu’on pensait alors vérifiée dans ce cas.
En 1955, ils écrivent un rapport interne dans lequel ils mentionnent que l’écriture de l’algorithme et la programmation du MANIAC I furent la tâche de Mary Tsingou (et à la rédaction duquel Fermi n’a pas participé à cause de sa mort prématurée en 1954).
Ces expériences ouvrirent la voie à toute une classe de problèmes nouveaux concernant les systèmes dynamiques non ergodiques et sont le point de départ de ce qui est maintenant une discipline à part entière : la physique numérique, qu’on peut considérer comme une branche intermédiaire entre la physique théorique et la physique expérimentale.
++++
4. La morphogenèse selon Alan Turing
Un des problèmes que s’était posé le biologiste D’Arcy Thompson est l’apparition de formes similaires pour des organismes non-apparentés, donc non explicables par des facteurs purement génétiques. Alan Turing postula qu’il devait y avoir un processus général à l’œuvre obéissant à des lois physico-chimiques. Il s’attela donc à la mise en place d’un modèle mathématique dont le but était de rendre compte de la « morphogenèse », c’est-à-dire, le passage d’un état d’équilibre initial symétrique, à un nouvel état d’équilibre non-symétrique qui constitue une forme. Ce passage devrait résulter d’une « réaction-diffusion » dans la chimie des composants du système.
Turing publie en 1952 un article célèbre intitulé « The chemical basis of morphogenesis » (Les fondements chimiques de la morphogenèse) dans lequel il propose un tel modèle et discute notamment deux exemples : la constitution de taches qui font penser à celle qu’on voit sur certains pelages d’animaux et l’hydre d’eau douce qui au cours de son développement initial développe de cinq à dix tentacules à partir d’une forme initiale tubulaire symétrique. Dans son article, Turing fait la plupart de ses calculs à la main mais montre un exemple numérique réalisé sur l’ordinateur de Manchester (le Manchester Mark I).
Du point de vue qui nous intéresse ici, Turing suggère que l’expérimentation numérique doit devenir un véritable instrument nouveau dans l’investigation de la nature. Il le confirme lui-même dans ses travaux ultérieurs consacrés à la botanique (plus précisément en phyllotaxie, c-à-d la disposition des feuilles le long des tiges des plantes). Terminons en mentionnant que les structures de Turing ont été obtenu dans une véritable expérience de chimie seulement en 1990 (V. Castets, E. Dulos, J. Boissonade and P. De Kepper, Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern, Phys. Rev. Lett. 64 (1990)).
Expérience Numérique Interactive
++++
5. Bryan Birch & Peter Swinnerton-Dyer & les points rationnels des courbes elliptiques
Cet exemple illustre l’apport de l’expérimentation numérique dans un domaine des mathématiques « pures » : la géométrie algébrique.

- Ordinateur EDSAC
Les mathématiciens ont toujours été fascinés par les équations algébriques dont on cherche des solutions qui sont des nombres entiers ou des nombres rationnels. C’est par exemple Euclide qui le premier a décrit toutes les solutions en nombres entiers de l’équation $x^2+y^2=z^2$. En divisant cette équation par $z^2$, cela revient à chercher les points de coordonnées rationnelles sur un cercle. La conjecture de Birch et Swinnerton-Dyer est reliée au nombre de points à coordonnées rationnelles d’un autre type de courbe : les courbes elliptiques. Elle est beaucoup trop technique pour être décrite ici.
Du point de vue qui nous intéresse, le fait remarquable est qu’elle a été émise au début des années 1960, par Birch et Swinnerton, grâce à des expériences numériques sur l’EDSAC (descendant de l’ENIAC) au laboratoire d’informatique de l’université de Cambridge. C’est l’un des sept problèmes du prix du millénaire proposés par le Clay Mathematical Institute en 2000 et il est à ce jour résolu que dans des cas particuliers.
++++
6. Edward Lorenz : de la météo aux attracteurs étranges

- Edward Lorenz
Au début des années 1960, Edward Lorenz étudie les phénomènes de convection dans l’atmosphère terrestre. Il travaille comme météorologue au Massachusetts Institute of Technology.
Il obtient un modèle de seulement trois équations différentielles couplées après avoir drastiquement simplifié les équations fournies par la physique. Nous ne tenterons pas de décrire ici ce que représentent ces équations. Le point qui nous intéresse est que Lorenz résout numériquement les équations et découvre ce qu’on a appelé par la suite le « chaos déterministe ».
Le phénomène de base est la « sensibilité » aux conditions initiales, autrement dit, le fait que d’infimes différences dans les conditions initiales produisent des trajectoires complètement différentes au bout d’un temps assez bref. L’observation capitale et remarquablement fine de Lorenz, compte-tenu de l’ordinateur qu’il avait à sa disposition (un Royal McBee LGP-300), est que les trajectoires ont beau dépendre des conditions initiales, elles semblent néanmoins s’accumuler sur une sorte de surface compliquée qui est insensible aux conditions initiales. Lorenz fait une esquisse de cet objet qui semble de dimension deux et dont s’approche rapidement la trajectoire d’une condition initiale. Elle voyage ensuite sur cette « surface » composée de deux sortes de lobes, passant de l’un à l’autre d’une manière qui semble aléatoire. Lorenz fait d’autres observations remarquablement inspirées que nous ne décrirons pas ici. Il venait d’observer le premier « attracteur étrange » comme allait le qualifier le physicien-mathématicien David Ruelle. Il s’agit d’un objet extraordinairement compliqué résultant pourtant de seulement trois équations différentielles couplées en apparence « innocente ».
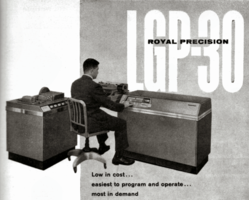
- Ordinateur Royal McBee "LGP-30"
Il convient de saluer l’extraordinaire intuition de Lorenz car ces observations pouvaient être interprétées comme un artefact de l’ordinateur. Cette question se pose encore aujourd’hui : il faut toujours faire attention que ce qu’on observe numériquement reflète correctement les équations sous-jacentes. Mais c’était pire à l’époque : les ordinateurs étaient extrêmement volumineux, bruyants, lents, chauffaient énormément et qui plus est, étaient beaucoup moins fiables qu’aujourd’hui.
Lorenz publia ses résultats en 1963 dans un journal de météorologie. Pour la petite histoire, notons que son article fut confié par le journal à Ulam pour évaluation. Il fallut près de dix ans avant que les physiciens et les mathématiciens ne réalisent l’importance de cet article. C’est en effet en 1972 que Lorenz présente l’effet papillon devant l’Association Américaine pour le progrès des Sciences avec une célèbre question : « Le battement d’aile d’un papillon au Brésil peut-il déclencher une tornade au Texas ? » Mais, surtout, Lorenz exhibe sur son écran d’ordinateur l’image surprenante de son attracteur.
Terminons en citant un extrait d’un article de Lorenz où il fait référence à Ulam juste après ces lignes :
« Nous voyons ainsi que l’ordinateur devrait jouer un rôle important, au-delà d’être un simple moulin à calculs. La machine ne peut pas prouver un théorème, mais elle peut suggérer une proposition à prouver. La proposition peut ensuite être prouvée et établie comme un théorème par des moyens analytiques, mais l’existence même du théorème pourrait ne pas être suspectée sans l’aide d’une machine. »
Lorenz, E. N. (1964), The problem of deducing the climate from the governing equations. Tellus, 16 : 1–11.
Citation originale de Lorenz :
« We thus see that a computing machine may play an important role, in addition to simply grinding out numerical answers. The machine cannot prove a theorem, but it can suggest a proposition to be proven. The proposition may then be proven and established as a theorem by analytical means, but the very existence of the theorem might not have been suspected without the aid of the machine. »
Attracteur de Lorenz en 3D
Nécessite WebGL dans votre navigateur). Vous pouvez faire tourner l’attracteur sur lui-même pour le voir sous toutes ses coutures.
++++
7. Martin Kruskal & Norman Zabusky découvrent numériquement les solitons


Au début des années 1960, les américains Martin Kruskal (physicien) et Norman Zabusky (mathématicien et physicien) reprennent le travail de Fermi-Pasta-Ulam en changeant le terme non linéaire qui régit l’interaction entre les ressorts. Avec leur programmeur, Gary Deem, ils procèdent à des expérimentations numériques qui les conduisent à l’observation d’un nouveau phénomène : des ondes « solitaires », qu’ils baptisent « solitons ». Deux solitons peuvent se rencontrer et repartir chacun de leur côté sans être modifiés ! Ces expériences numériques sont menées au Bell Telephone Laboratory à Whippany, sur des machines IBM 709 et 7090.
Kruskal et Zabusky réalisent qu’une approximation continue de ce problème n’est rien d’autre qu’une équation aux dérivées partielles qui avait été introduite par Diederik Korteweg et son étudiant Gustav de Vries en 1895. Leur but était d’expliquer les vagues « bizarres » observées cinquante ans plus tôt par l’ingénieur écossais John Scott Russel dans un canal.
C’est donc indirectement le travail de Fermi-Pasta-Ulam, repris par Kruskal et Zabusky, qui fait sortir de l’oubli l’équation de Korteweg-de Vries après près de soixante-dix ans de sommeil. L’expérimentation numérique a permis l’observation de solutions inattendues. Tout un pan de la physique et des mathématiques venait de naitre.
Dans l’approche de Kruskal et Zabusky, la visualisation joue un rôle crucial. Ceci nous paraît banal aujourd’hui mais ce n’était pas le cas à cette époque : ils ont non seulement du inventer leurs propres outils de visualisation, mais aussi d’interaction avec le programme. Pour eux, l’expérimentation numérique interactive dépasse le simple outil : le fait de modifier « en temps réel » des paramètres et de visualiser presqu’aussitôt le résultat, puis d’éventuellement recommencer, développe un rapport et une intuition nouveaux avec les équations.
++++
8. Michel Hénon : de l’astrophysique aux attracteurs étranges

- Michel Hénon
Michel Hénon a placé au cœur de sa pratique scientifique les expériences numériques qu’il considérait comparable aux expériences de physique. Il s’intéresse à l’astrophysique qui est un domaine où l’expérimentation directe est bien sûr impossible ! Le calcul numérique est la seule façon de faire des « expériences ».
Dans les années 1950, Hénon participe à la construction de calculateurs analogiques puis en construit entièrement un pour son propre usage qu’il abandonnera avec l’avènement et la démocratisation des ordinateurs numériques. Il utilisera l’IBM 750 à l’observatoire de Meudon, l’IBM 7040 de l’observatoire de Nice ou encore la toute première calculatrice scientifique programmable de poche : la HP65.

- Michel Hénon devant son calculateur analogique, construit avec Michel Dreux
Dans les années 1960, Hénon s’interresse à différents problèmes d’astrophysique. Durant son séjour à Princeton, en 1962, il projette d’étudier le problème d’une étoile dans une galaxie asymétrique. Il réalise plusieurs expériences numériques qui révèlent des « irrégularités ». Il confie à un étudiant, Carl Heiles, la tâche refaire ses calculs, sur une autre machine, indépendamment, comme on ferait avec une expérience de physique dont on exige qu’elle soit reproductible. Ces résultats conduiront à l’article de Hénon et Heiles de 1964 qui révèle un mélange de comportements quasi-périodiques et « ergodiques ».
L’astronomie étant une discipline très mathématisée, Hénon propose de se concentrer sur les propriétés mathématiques de modèles simples obtenus par des méthodes bien connues (datant de Poincaré et Birkhoff) qui conduisent à remplacer les équations différentielles par des itérations en utilisant des « sections transverses » habilement choisies. Malgré leur simplicité, ces modèles restent extrêmement difficiles à étudier analytiquement. Hénon propose donc de faire un usage systématique des expériences numériques.

- Attracteur de Hénon extrait de son article
Une illustration éclatante de sa démarche concerne le problème restreint des trois corps. Hénon montre comment mettre en pratique les idées de Poincaré et Birkhoff pour explorer systématiquement le comportement des trajectoires possibles.
Le travail pour lequel Hénon est sans doute le plus connu en dehors de l’astronomie est celui sur l’attracteur étrange qui porte son nom. En jouant sur les paramètres des équations de Lorenz et en utilisant une section de Poincaré, Yves Pomeau, qui réalise une série de calculs numériques avec J. L. Ibanez, met en évidence le mécanisme de formation d’un « fer à cheval » de S. Smale. Pomeau expose ses travaux lors d’un séminaire donné à l’Observatoire de la Côte d’Azur auquel assiste Michel Hénon. Ce dernier propose alors un modèle très simple de transformation quadratique du plan qui simule, lorsqu’un paramètre varie, le mécanisme de formation d’un fer à cheval : c’est le fameux modèle de Hénon. L’exploration numérique de ce modèle montre, pour certaines valeurs des paramètres, l’existence d’un « attracteur étrange ». Le fait que cet attracteur existe vraiment, c-à-d qu’il n’est pas un artefact numérique, est resté un problème ouvert jusqu’en 1991. Ce sont les mathématiciens suédois Benedicks et Carleson qui, les premiers, ont démontré mathématiquement l’existence de tels objets.
++++
9. La cascade de doublements de période : Mitchell Feigenbaum, Pierre Coullet & Charles Tresser

- Pierre Coullet
En 1978, Pierre Coullet, jeune chercheur au CNRS à l’Université de Nice et Charles Tresser, étudiant en 3ème cycle, s’intéressent au mécanisme de transition vers la turbulence et en particulier à sa modélisation par des systèmes dynamiques simples, comme l’itération d’une application de l’intervalle. Comme pour le modèle de Hénon, l’exploration numérique a joué un grand rôle dans leurs travaux. La nouveauté réside dans une approche « interactive » de l’expérimentation numérique : la visualisation du résultat obtenu en « temps réel » pour une valeur du paramètre permet de faire de nouveaux choix des valeurs des paramètres et de se forger ainsi une intuition du phénomène.

- Feigenbaum et Cvitanović devant une machine Sun
En même temps que Mitchell Feigenbaum, et indépendamment de lui, ils ont eu l’idée d’appliquer les techniques du groupe de renormalisation aux problèmes de la transition vers le chaos pour les applications « unimodales » (c-à-d avec une seule « bosse ») de l’intervalle. Plus précisément ils montrent que la transition vers le chaos pour les applications unimodales se fait par une cascade de doublements de période qui possède des propriétés géométriques universelles. Par exemple les valeurs du paramètre pour lesquelles on assiste à un doublement de période s’accumulent avec une raison géométrique indépendante du modèle d’applications que l’on étudie.
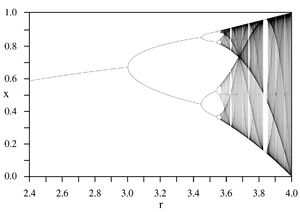 Au moyen d’un ordinateur HP9825 et d’un traceur XY, Coullet et Tresser ont pu visualiser les itérations de l’application logistique, changer de paramètre et visualiser immédiatement le résultat de ce changement.
Le langage HPL, proche du Basic, permettait de modifier la valeur d’une variable au clavier, sans interrompre le programme. Notons que Feigenbaum a de son côté utilisé la calculatrice programmable HP65, le même modèle que Michel Hénon pour son attracteur.
Au moyen d’un ordinateur HP9825 et d’un traceur XY, Coullet et Tresser ont pu visualiser les itérations de l’application logistique, changer de paramètre et visualiser immédiatement le résultat de ce changement.
Le langage HPL, proche du Basic, permettait de modifier la valeur d’une variable au clavier, sans interrompre le programme. Notons que Feigenbaum a de son côté utilisé la calculatrice programmable HP65, le même modèle que Michel Hénon pour son attracteur.
On peut se demander s’il est possible d’observer une transition vers le chaos par une cascade de de doublements de période dans une vraie expérience de physique. La réponse est positive : en 1979, Albert Libschaber observa la convection dans l’helium liquide, en augmentant peu à peu le paramètre de contrôle que constitue la différence de température entre le bas et la haut de la cellule de convection. Il observa effectivement une transition vers le chaos suivant ce schéma.
Terminons en mentionnant que la reconnaissance accordée à Coullet et Tresser n’est pas à la hauteur de leur véritable contribution. Une analyse de cet état de fait est proposée dans la thèse de L. Petitgirard (chapitre 5).
++++
10. Itérations de polynômes complexes : Benoît Mandelbrot, John Hubbard & Adrien Douady

- Benoît Mandelbrot
Nous évoquerons pour terminer la dynamique complexe, un domaine défriché par les mathématiciens français Pierre Fatou et Gaston Julia au début du 20ème siècle, mais qui doit son réveil, après environ une soixante d’années d’hibernation, à l’expérimentation numérique. En effet, la visualisation des ensembles de Julia a été une révélation qui a permis aux mathématiciens de se poser les bonnes questions.
Dans la préface du livre The Mandelbrot set, theme and variations, le mathématicien John Hubbard explique comment l’enseignement en DEUG, en 1976-77, à l’université d’Orsay, l’a amené à faire des expériences numériques. En cherchant comment utiliser un ordinateur dans le cadre de son cours d’analyse, il choisit d’illustrer la méthode de Newton. Comme son domaine de recherche est l’analyse complexe, il l’applique à un polynôme complexe, par exemple $z^3-1$, pour visualiser les bassins d’attraction des racines. Il se fait aider par Michel Fiollet pour écrire des programmes sur une mini-6. Stimulé par le mathématicien Dennis Sullivan qui se trouve à l’IHES (Bures-sur-Yvette), il explore et visualise divers « ensembles de Julia » : étant donné deux nombres complexes $z_0$ et $c$, on définit la suite $(z_n)$ par récurrence en posant ![]() . Pour une valeur donnée de c, l’ensemble de Julia correspondant est la frontière de l’ensemble des valeurs initiales $z_0$ pour lesquelles la suite est bornée.
. Pour une valeur donnée de c, l’ensemble de Julia correspondant est la frontière de l’ensemble des valeurs initiales $z_0$ pour lesquelles la suite est bornée.
Il semble que Hubbard ait montré ses images durant une conférence à laquelle assiste Benoît Mandelbrot, en 1997, aux USA. Ce dernier lui dit avoir souvent pensé à ces ensembles sans jamais avoir cherché à en obtenir des images. Hubbard mentionne qu’en 1981-82, l’arrivée de l’Apple II va énormément compter pour lui et lui permet d’obtenir de bien meilleures images qu’auparavant.
Alors que Mandelbrot travail chez IBM et a accès aux meilleurs ordinateurs de l’époque, c’est lors d’un séjour à Harvard, qu’il obtient pour la première fois en mars 1980 une visualisation grossière au moyen d’un ordinateur Vax de l’ensemble qui portera son nom.
Il est obtenu en traçant l’ensemble de toutes les valeurs de $c$ pour lesquelles la suite définie ci-dessus est bornée, en prenant $z_0=0$ . Le programmeur est Peter Moldave. Il publie un article sur ses résultats la même année.
L’étude de l’ensemble de Mandelbrot commence réellement en 1984 avec les travaux de Douady et Hubbard, qui établissent ses propriétés fondamentales et baptisent l’ensemble en l’honneur de Mandelbrot. Hubbard utilise beaucoup d’expériences numériques pour guider leur intuition.
En 1985, les mathématiciens Heinz-Otto Peitgen et Peter Richter popularisent l’ensemble de Mandelbrot par des images de qualité et qui frappent les esprits.
++++
Quelques références bibliographiques
![]() H. L. Anderson. Scientific uses of the MANIAC. J. Stat. Phys. vol. 43, 1986.
H. L. Anderson. Scientific uses of the MANIAC. J. Stat. Phys. vol. 43, 1986.
![]() J. Borwein & D. Bailey. Mathematics by Experiment : Plausible Reasoning in the 21st Century (2008, Second Edition) & Experimentation in Mathematics : Computational Paths to Discovery (2004). A K Peters. On peut consulter le site : http://www.experimentalmath.info
J. Borwein & D. Bailey. Mathematics by Experiment : Plausible Reasoning in the 21st Century (2008, Second Edition) & Experimentation in Mathematics : Computational Paths to Discovery (2004). A K Peters. On peut consulter le site : http://www.experimentalmath.info
![]() M. Farge. L’approche numérique : Simulation ou simulacre des phenomènes ? in `Logos et Théorie des Catastrophes’, éd. Jean Petitot, Patino, 119-139 (1988).
M. Farge. L’approche numérique : Simulation ou simulacre des phenomènes ? in `Logos et Théorie des Catastrophes’, éd. Jean Petitot, Patino, 119-139 (1988).
![]() J. Hubbard, préface de : The Mandelbrot set, theme and variations. Edited by Lei Tan. London Math. Soc. Lecture Note Ser., 274. Cambridge University Press, 2000.
J. Hubbard, préface de : The Mandelbrot set, theme and variations. Edited by Lei Tan. London Math. Soc. Lecture Note Ser., 274. Cambridge University Press, 2000.
![]() E. N. Lorenz. Predictability : does the flap of a butterfly’s wings in Brazil set off a tornado in Texas ? 139th Annual Meeting of the American Association for the Advancement of Science (29 Dec 1972), in Essence of Chaos (1995), Appendix 1, p. 181.
E. N. Lorenz. Predictability : does the flap of a butterfly’s wings in Brazil set off a tornado in Texas ? 139th Annual Meeting of the American Association for the Advancement of Science (29 Dec 1972), in Essence of Chaos (1995), Appendix 1, p. 181.
![]() B. Mandelbrot. Fractals and the Rebirth of Iteration Theory. In : Peitgen & Richter : The Beauty of Fractals (1986), pp 151-160.
B. Mandelbrot. Fractals and the Rebirth of Iteration Theory. In : Peitgen & Richter : The Beauty of Fractals (1986), pp 151-160.
![]() L. Petitgirard. Le chaos : des questions théoriques aux enjeux sociaux. Thèse de doctorat, Univ. Lyon 2, 2004. Cf. chapitre 9.
L. Petitgirard. Le chaos : des questions théoriques aux enjeux sociaux. Thèse de doctorat, Univ. Lyon 2, 2004. Cf. chapitre 9.
![]() S. Ulam. Science, computers, and people. Birkhäuser Boston, Inc., Boston, MA, 1986. Lire en particular le chapter 6 (« Computers in Mathematics »), 9 (« Patterns of growth of figures ») & 17 (« Von Neumann : The Interaction of Mathematics and Computing »).
S. Ulam. Science, computers, and people. Birkhäuser Boston, Inc., Boston, MA, 1986. Lire en particular le chapter 6 (« Computers in Mathematics »), 9 (« Patterns of growth of figures ») & 17 (« Von Neumann : The Interaction of Mathematics and Computing »).
![]() T. Weissert. The genesis of simulation in dynamics. Pursuing the Fermi-Pasta-Ulam problem. Springer-Verlag, New York, 1997. Cf. Chapitre 5 : Steps to an Epistemology of Simulation.
T. Weissert. The genesis of simulation in dynamics. Pursuing the Fermi-Pasta-Ulam problem. Springer-Verlag, New York, 1997. Cf. Chapitre 5 : Steps to an Epistemology of Simulation.
![]() N. Zabusky. Fermi-Pasta-Ulam, Solitons and the Fabric of Nonlinear and Computational Science : History, Synergetics and Visiometrics. Chaos vol. 15, 2005.
N. Zabusky. Fermi-Pasta-Ulam, Solitons and the Fabric of Nonlinear and Computational Science : History, Synergetics and Visiometrics. Chaos vol. 15, 2005.
++++
Références « historiques », pour ceux qui veulent lire certains des travaux originels mentionnés dans le texte
![]() B. J. Birch, H. P. F. Swinnerton-Dyer. Notes on elliptic curves. I. J. Reine Angew. Math. vol. 212, 1963.
B. J. Birch, H. P. F. Swinnerton-Dyer. Notes on elliptic curves. I. J. Reine Angew. Math. vol. 212, 1963.
![]() P. Coullet, C. Tresser. Itérations d’endomorphismes et groupe de renormalisation. Le Journal de Physique vol. 35, 1978.
P. Coullet, C. Tresser. Itérations d’endomorphismes et groupe de renormalisation. Le Journal de Physique vol. 35, 1978.
![]() M. Feigenbaum. Quantitative Universality for a Class of Non-Linear Transformations. J. Stat. Phys. vol. 19, 1978.
M. Feigenbaum. Quantitative Universality for a Class of Non-Linear Transformations. J. Stat. Phys. vol. 19, 1978.
![]() E. Fermi, J. Pasta et S. Ulam. Studies of Nonlinear Problems. Document Los Alamos 1940 (May 1955).
E. Fermi, J. Pasta et S. Ulam. Studies of Nonlinear Problems. Document Los Alamos 1940 (May 1955).
![]() M. Hénon, C. Heiles. The applicability of the third integral of motion : Some numerical experiments. The Astrophysical Journal 69 (1964).
M. Hénon, C. Heiles. The applicability of the third integral of motion : Some numerical experiments. The Astrophysical Journal 69 (1964).
![]() M. Hénon. A two-dimensional mapping with a strange attractor. Comm. Math. Phys. vol. 50, 1976.
M. Hénon. A two-dimensional mapping with a strange attractor. Comm. Math. Phys. vol. 50, 1976.
![]() E. N. Lorenz. Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences vol. 20, 1963.
E. N. Lorenz. Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences vol. 20, 1963.
![]() B. Mandelbrot. Fractal aspects of the iteration of $z\mapsto \lambda z(1-z)$ for complex $\lambda$ and $z$. Ann. New York Acad. Sci. 357 (1980).
B. Mandelbrot. Fractal aspects of the iteration of $z\mapsto \lambda z(1-z)$ for complex $\lambda$ and $z$. Ann. New York Acad. Sci. 357 (1980).
![]() A. Turing. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society B (1952).
A. Turing. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society B (1952).
![]() N. J. Zabusky, M. D. Kruskal. Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States. Phys. Rev. Lett. vol. 15 (1965).
N. J. Zabusky, M. D. Kruskal. Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States. Phys. Rev. Lett. vol. 15 (1965).
![]() G. S. Deem, N. J. Zabusky, M. D. Kruskal. Formation, Propagation, and Interaction of Solitons : Numerical Solutions of Differential Equations Describing Wave Motion in Nonlinear Dispersive Media. Film Library of the Bell Telephone Laboratories, Inc., Whippany, NJ.
G. S. Deem, N. J. Zabusky, M. D. Kruskal. Formation, Propagation, and Interaction of Solitons : Numerical Solutions of Differential Equations Describing Wave Motion in Nonlinear Dispersive Media. Film Library of the Bell Telephone Laboratories, Inc., Whippany, NJ.
++++








